SISTEM BILANGAN,KONVERSI BILANGAN,GERBANG LOGIKA,MULTIPLEXER,DECODER,ENCODER,DAN FLIP FLOP.

SISTEM BILANGAN,KONVERSI BILANGAN,GERBANG LOGIKA,MULTIPLEXER,DECODER,ENCODER,DAN FLIP FLOP.

                 Adalah suatu proses dimana satu system bilangan dengan basis tertentu akan dijadikan bilangan dengan basis yang lain.

Macam - macam Sistem Bilangan :

Bilangan desimal  ADALAH bilangan yang menggunakan 10 angka mulai 0 sampai 9 berturut2. Setelah angka  9, maka angka berikutnya adalah 10, 11, 12 dan seterusnya. Bilangan desimal disebut juga bilangan berbasis 10. Contoh penulisan bilangan desimal : 17₁₀. Ingat, desimal berbasis 10, maka angka 10-lah yang menjadisubscript pada penulisan bilangan desimal.

Bilangan biner ADALAH bilangan yang hanya menggunakan 2 angka, yaitu 0 dan 1. Bilangan biner juga disebut bilangan berbasis 2. Setiap bilangan pada bilangan biner disebut bit, dimana 1 byte = 8 bit.  Contoh penulisan : 110111₂.

    

Bilangan octal ADALAH bilangan berbasis 8, yang menggunakan angka 0 sampai 7. Contoh penulisan : 17₈.

Bilangan hexadesimal ADALAH ilangan heksa, atau bilangan basis 16, menggunakan 16  buah simbol, mulai dari 0 sampai 9, kemudian dilanjut dari A sampai F. Jadi, angka A sampai F merupakan simbol untuk 10 sampai 15. Contoh penulisan : C5₁₆.

Konversi bilangan

A. BINER

Konversi bilangan biner ke desimal

Contoh : 110001₂ diubah menjadi bilangan Desimal

110001₂= ( 1 x 2⁵ ) + ( 1 x 2⁴ ) + ( 0 x 2³ ) + ( 0 x 2² ) + ( 0 x 2¹) + ( 1 x 2⁰ )

= 32 + 16 + 0 + 0 + 0 + 1

= 49

Jadi, 11001₂ = 49

Konversi bilangan Biner ke Octal

Contoh : 11110011001₂ diubah menjadi bilangan Oktal menjadi

11 110 011 001 = 11₂ = 2¹ + 2⁰ = 3₈

= 110₂ = 2² + 2¹ = 6₈

= 011₂ = 2¹ + 2⁰ = 3₈

= 001₂ = 2⁰ =1₈

Jadi, 11110011001₂ = 3631₈

Konversi bilangan Biner ke Hexadecimal 

Contoh: 0100111101011100₂ diubah menjadi bilangan HexaDesimal

0100 1111 0101 1100 = 0100₂ = 2² = 4₁₆

= 1111₂ = 2³ + 2² + 2¹ + 2⁰ = 15 - F₁₆

= 0101₂ = 2² + 2⁰ = 5₁₆

= 1100₂ = 2³ + 2² = 12 - C₁₆

Jadi, 0100111101011100₂ = 4F5C₁₆

A. OKTAL

  

a. Oktal ke Biner 

Cara mengubah bilangan Oktal menjadi Biner dengan menjadikan satu persatu angka bilangan Oktal menjadi bilangan Biner dahulu kemudian di satukan. Untuk bilangan Oktal haruslah memiliki 3 digit bilangan Biner sehingga jika hanya menghasilkan kurang dari 3 digit makan didepannya ditambahkan bilangan 0.

Contoh : 261₈ diubah menjadi bilangan Biner

261 = 2₈ = 010₂

= 6₈ = 110₂

= 1₈ = 001₂

Jadi, 261₈ = 010110001₂ 

 b. Oktal ke Desimal

Cara mengubah bilangan Oktal menjadi bilangan Desimal dengan mengubah bilangan Oktal tersebut menjadi bilangan Biner terlebih dahulu baru kita ubah menjadi bilangan Desimal.

Contoh : 2618 diubah menjadi bilangan Desimal

Langkah 1 : mengubah ke bilangan Biner

261 = 2₈ = 010₂

= 6₈ = 110₂

= 1₈ = 001₂

Jadi, 261₈ = 010110001₂

Langkah 2 : mengubah bilangan Biner menjadi Desimal

010110001₂ = ( 0 x 2⁸ ) + ( 1 x 2⁷ ) + ( 0 x 2⁶ ) + ( 1 x 2⁵ ) + ( 1 x 2⁴ ) + ( 0 x 2³ ) + ( 0 x 2² ) + ( 0 x 2¹ ) + ( 1 x 2⁰ )

= 0 + 128 + 0 + 32 + 16 + 0 + 0 + 0 + 1

= 177

Jadi, 261₈ = 177

c.  

b. Oktal ke HexaDesimal

Cara mengubah bilangan Oktal menjadi bilangan HexaDesimal dengan mengubah bilangan Oktal tersebut menjadi bilangan Biner terlebih dahulu baru kita ubah menjadi bilangan Desimal. Lalu kita ubah lagi menjadi bilangan HexaDesimal.

Contoh : 261₈ diubah menjadi bilangan HexaDesimal

Langkah 1 : mengubah ke bilangan Biner

261 = 2₈ = 010₂

= 6₈ = 110₂

= 1₈ = 001₂

Jadi, 261₈ = 010110001₂

Langkah 2 : mengubah bilangan Biner menjadi Desimal

010110001₂ = ( 0 x 2⁸ ) + ( 1 x 2⁷ ) + ( 0 x 2⁶ ) + ( 1 x 2⁵ ) + ( 1 x 2⁴ ) + ( 0 x 2³ ) + ( 0 x 2² ) + ( 0 x 2¹ ) + ( 1 x 2⁰ )

= 0 + 128 + 0 + 32 + 16 + 0 + 0 + 0 + 1

= 177

Langkah 3 : mengubah bilangan Desimal menjadi HexaDesimal

177 kita bagi dengan 16 - 117:16 = 11 sisa 1

11 : 16 = 0 sisa 11 - B

dibaca dari bawah maka menjadi B1

Jadi 261₈ = B1₁₆

_{C. DESIMAL}

a. Desimal ke Biner

Cara mengubah bilangan Desimal menjadi Biner yaitu dengan membagi bilangan Desimal dengan angka 2 dan tulis sisanya mulai dari bawah ke atas.

Contoh : 25 diubah menjadi bilangan Biner

25 : 2 = 12 sisa 1

12 : 2 = 6 sisa 0

6 : 2 = 3 sisa 0

3 : 2 = 1 sisa 1

1 : 2 = 0 sisa 1

maka ditulis 11001

Jadi 25 = 11001₂

b. Desimal ke Oktal

Cara mengubah bilangan Desimal menjadi Oktal yaitu dengan membagi bilangan Desimal dengan angka 8 dan tulis sisanya mulai dari bawah ke atas.

Contoh : 80 diubah menjadi bilangan Oktal

80 : 8 = 10 sisa 0

10 : 8 = 1 sisa 2

1 : 8 = 0 sisa 1

maka ditulis 120

Jadi 80 = 120₈

c. Desimal ke HexaDesimal

Cara mengubah bilangan Desimal menjadi HexaDesimal yaitu dengan membagi bilangan Desimal dengan angka 16 dan tulis sisanya mulai dari bawah ke atas.

Contoh : 275 diubah menjadi bilangan HexaDesimal

275 : 16 = 17 sisa 3

17 : 16 = 1 sisa 1

1 : 16 = 0 sisa 1

maka ditulis 113

Jadi 275 = 113₁₆

_{D. HexaDesimal}

a. HexaDesimal ke Biner

Cara mengubah bilangan HexaDesimal menjadi Biner dengan menjadikan satu persatu angka bilangan HexaDesimal menjadi bilangan Biner dahulu kemudian di satukan. Untuk bilangan HexaDesimal haruslah memiliki 4 digit bilangan Biner sehingga jika hanya menghasilkan kurang dari 4 digit makan didepannya ditambahkan bilangan 0.

Contoh : 4DA2₁₆ diubah menjadi bilangan Biner

4DA2 = 4₁₆ = 0100₂

= D₁₆ = 1101₂

= A₁₆ = 1010₂

= 2₁₆ = 0010₂

Jadi 4DA2₁₆ = 0100110110100010₂

b. HexaDesimal ke Desimal

Cara mengubah bilangan biner menjadi bilangan desimal dengan mengalikan 16ⁿ dimana n merupakan posisi bilangan yang dimulai dari angka 0 dan dihitung dari belakang.

Contoh : 3C2₁₆ diubah menjadi bilangan Desimal

3C2₁₆ = ( 3 x 16² ) + ( C(12) x 16¹) + ( 2 x 16⁰ )

= 768 + 192 + 2

= 962

Jadi 3C2₁₆ = 962

c. HexaDesimal ke Oktal

Cara mengubah bilangan HexaDesimal menjadi bilangan Oktal dengan mngubah bilangan HexaDesimal tersebut menjadi bilangan Desimal terlebih dahulu baru kita ubah menjadi bilangan Oktal.

Contoh : 3C2₁₆ diubah menjadi bilangan Oktal

Langkah 1: Mengubah bilangan HexaDesimal menjadi Desimal

3C2₁₆ = ( 3 x 16² ) + ( C(12) x 16¹) + ( 2 x 16⁰ )

= 768 + 192 + 2

= 962

Langkah 2 : Mengubah bilangan Desimal menjadi Oktal

962 : 8 = 120 sisa 2

120 : 8 = 15 sisa 0

15 : 8 = 1 sisa 7

1 : 8 = 0 sisa 1

maka ditulis 1702

Jadi 3C2₁₆ = 1702₈

Konversi dan Sistem Bilangan

I . Konversi dan Sistem Bilangan Desimal 

Konversi Ke Sistem Bilangan Binari 

Contoh : 

Bilangan desimal 45 dikonversi ke bilangan binar

20 = 1

22 = 4

23 = 8

25 = 32

--+ --+

45 101101

Konversi ke Bilangan Oktal 

Untuk mengkonversi bilangan desimal ke bilangan oktal dapat digunakan remainder method dengan pembaginya adalah basis dari bilagan Oktal yaitu 8 

Contoh 

385 : 8 = 48 sisa 1

48 : 8 = 6 sisa 0

Konversi ke Bilangan Hexadesimal dengan menggunakan remainder metode dibagi dengan basis bilangan hexadesimal yaitu 16

Contoh 

1583 : 16 = 98 sisa 15 = F

98 : 16 = 6 sisa 2

II. Konversi dari Sistem Bilangan Binari 

Konversi ke sistem bilangan desimal dari bilangan binari dapat dikonversikan ke bilangan desimal dengan cara mengalikan masing-masing bit dalam bilangan dengan position value-nya.

Contoh : 

1011012 = 1 x 25 + 0 x 24 + 1 x 20 + 1 x 22 + 0 x 21 + 1 x 20

= 32 + 0 + 8 + 4 + 0 + 1

= 4510

Konversi ke sistem bilangan oktal Konversi dari bilangan binary ke oktal dapat dilakukan dengan mengkonversi tiap tiga buat digit binari

Contoh :1101101 dapat dikonversi ke oktal dengan cara : 

1 = 1 101 = 5 101 = 5

Konversi ke sistem bilangan hexadesimal Konversi dari bilangan binary ke hexadesimal dapat dilakukan dengan mengkonversi tiap empat buat digit binari

Contoh : 1101101 dapat dikonversi ke hexadecimal dengan 

110 = 6 1101 = D

III. Konversi dari Sistem Bilangan Oktal 

Konversi ke sistem bilangan desimal dari bilangan binari dapat dikonversikan ke bilangan desimal dengan cara mengalikan masing-masing bit dalam bilangan dengan position value-nya.

Contoh : 

3248 = 3 x 82 + 2 x 81 + 4 x 80

= 3 x 64 + 2 x 8 + 4 x 1

= 192 + 16 + 4

= 212 10 

Konversi dari bilangan Oktal ke Binari dapat dilakukan dengan mengkonversi masing-masing digit oktal ke 3 digit binari.

Contoh : 

5 = 101 6 = 110 7=111 dapat dikonversi ke binari dengan cara :

Konversi dari bilangan oktal ke hexadesimal dapat dilakukan dengan cara merubah dari bilangan oktal menjadi bilangan binari terlebih dahulu, baru dikonversi ke bilangan hexadesimal 

Contoh : 

5 = 101 6 = 110 7 = 111 dikonversi terlebih dahulu ke binari

dari bilangan binar baru dikonversi ke hexadesimal 

1 = 7 0111 = 7 0111 = 7

IV. Konversi dari Sistem Bilangan Heksadesimal 

Konversi ke sistem bilangan desimal dari bilangan binari dapat dikonversikan ke bilangan desimal dengan cara mengalikan masing-masing bit dalam bilangan dengan position value-nya.

Contoh : 

B6A16 = 11 x 162 + 6 x 161 + 10 x 160

= 11 x 256 + 6 x 16 + 10 x 1

= 2816 + 96 + 10

= 292210

Konversi dari bilangan hexadesimal ke Binari dapat dilakukan dengan mengkonversi masing-masing digit hexadesimal ke 4 digit binari.

Contoh : 

D = 1101 6 = 0110

Konversi dari bilangan hexadesimal ke oktal dapat dilakukan dengan cara merubah ke bilangan binar terlebih dahulu baru dikonversi ke oktal.

Contoh : 

D = 1101 6 = 0110

Kemudian dikonversi ke bilangan oktal

11 = 3 010 = 2 110 = 6

Gerbang logika

Gerbang logika atau gerbang logik adalah suatu entitas dalam elektronika dan matematika Boolean yang mengubah satu atau beberapa masukan logik menjadi sebuah sinyal keluaran logik. Gerbang logika terutama diimplementasikan secara elektronis menggunakan diode atau transistor, akan tetapi dapat pula dibangun menggunakan susunan komponen-komponen yang memanfaatkan sifat-sifat elektromagnetik (relay), cairan, optik dan bahkan mekanik.

GERBANG ELEKTRONIKA

Untuk membangun sistem logika yang berfungsi secara penuh, relay, tabung hampa, atau transistor dapat digunakan. Contoh gerbang logika yaitu logika resistor-transistor (resistor-transistor logic / RTL), logika diode–transistor (diode-transistor logic / DTL), logika transistor-transistor (transistor-transistor logic / TTL), dan logika complementary metal–oxide–semiconductor (CMOS).

Multiplekser Multiplekser atau disingkat MUX adalah alat atau komponen elektronika yang bisa memilih input (masukan) yang akan diteruskan ke bagian output (keluaran). Pemilihan input mana yang dipilih akan ditentukan oleh signal yang ada di bagian kontrol (kendali) Select Komponen yang berfungsi kebalikan dari MUX ini disebut Demultiplekser (DEMUX). Pada DEMUX, jumlah masukannya hanya satu, tetapi bagian keluarannya banyak. Signal pada bagian input ini akan disalurkan ke bagian output (channel) yang mana tergantung dari kendali pada bagian SELECTnya. Dekoder biner Dalam digital electronics , sebuah decoder biner adalah rangkaian logika kombinasional yang mengubah nilai biner integer ke pola bit output yang terkait. Mereka digunakan dalam berbagai macam aplikasi, termasuk data demultiplexing , seven segment display, dan alamat memori decoding. Ada beberapa jenis dekoder biner, namun dalam semua kasus, decoder adalah rangkaian elektronik dengan banyak masukan dan beberapa sinyal keluaran, yang mengubah setiap kombinasi unik dari keadaan input menjadi kombinasi tertentu dari keadaan keluaran. Selain input data integer, beberapa decoder juga memiliki satu atau lebih input "enable". Bila input memungkinkan dinegasikan (dinonaktifkan), semua keluaran dekoder dipaksa ke keadaan tidak aktif mereka. Bergantung pada fungsinya, sebuah dekoder biner akan mengubah informasi biner dari n sinyal input menjadi 2 n sinyal keluaran unik. Beberapa decoder memiliki garis output kurang dari 2 n ; Dalam kasus tersebut, setidaknya satu pola output akan diulang untuk nilai masukan yang berbeda. Sebuah dekoder biner biasanya diimplementasikan sebagai sirkuit terpadu yang berdiri sendiri (IC) atau sebagai bagian dari IC yang lebih kompleks. Dalam kasus terakhir, decoder dapat disintesis dengan menggunakan bahasa deskripsi perangkat keras seperti VHDL atau Verilog . Dekoder yang sering digunakan sering tersedia dalam bentuk IC standar. ISI 1Jenis dekoder 1.1decoder 1-of-n 1.2Kode penerjemah 2Lihat juga Decoder 1-of-n  Contoh tipe decoder ini meliputi:Sebuah dekoder biner 1-of-n memiliki n bit output. Jenis decoder ini menegaskan dengan tepat salah satu dari n bit outputnya, atau tidak satupun dari keduanya, untuk setiap nilai input integer. "Alamat" (nomor bit) dari output yang diaktifkan ditentukan oleh nilai input integer.Misalnya, bit output 0 dipilih saat nilai integer 0 diterapkan pada input. Sebuah decoder baris 3-ke-8 mengaktifkan satu dari delapan bit output untuk setiap nilai masukan dari 0 sampai 7 - kisaran nilai integer yang dapat dinyatakan dalam tiga bit. Demikian pula, decoder baris 4 sampai 16 akan mengaktifkan satu dari 16 output untuk setiap input 4 bit pada kisaran bilangan bulat [0,15]. BCD ke desimal decoder memiliki sepuluh bit output. Ini menerima nilai masukan yang terdiri dari nilai bilangan desimal desimal binerdan mengaktifkan satu keluaran unik dan unik untuk setiap nilai masukan di kisaran [0,9]. Semua output tidak aktif saat nilai non-desimal diterapkan pada input. Demultiplexer adalah dekoder biner 1-of-n yang digunakan untuk mengarahkan bit data ke salah satu keluaran n sementara output lainnya tetap tidak aktif. Code translator  Penerjemah kode berbeda dari dekoder 1-of-n dalam beberapa bit output mungkin aktif pada saat bersamaan. Contoh dari hal ini adalah decoder tujuh segmen , yang mengubah bilangan bulat menjadi kombinasi sinyal kontrol segmen yang diperlukan untuk menampilkan nilai integer pada digit display tujuh segmen . Salah satu varian decoder tujuh segmen adalah BCD sampai tujuh segmen decoder , yang menerjemahkan nilai desimal kode biner ke dalam sinyal kontrol segmen yang sesuai untuk nilai integer masukan 0 sampai 9. Fungsi dekoder ini tersedia di IC standar . Encoder Encoder adalah alat, sirkuit, transduser, program perangkat lunak, algoritma atau orang yang mengubah informasi dari satu format atau kode ke kode lainnya, untuk keperluan standardisasi, kecepatan atauan. penekan ISI 1contoh 1.1Media 1.2posisi pekerjaan 1.3Perangkat lunak pengkodean medis 1.4Transduser 1.5Telekomunikasi 1.6Sirkuit elektronik 2Lihat juga 3Pranala luar CONTOH  Media  Perangkat lunak untuk mengkodekan audio , video , gambar, atau teks ke dalam format standar: Kompresor mengkodekan data (misalnya, audio / video / gambar) ke dalam bentuk yang lebih kecil (lihat codec ) Encoder audio mengubah audio analog menjadi sinyal audio digital Encoder video mengubah video analog menjadi sinyal video digital Encoder email mengamankan alamat email online dari pemanen email Encoder PHTML mempertahankan logika kode script dalam format aman yang transparan bagi pengunjung di situs web Multiplexer menggabungkan beberapa input menjadi satu output Encoder 8b / 10b digunakan untuk kecepatan cepat dalam sistem komunikasi Posisi pekerjaan  Encoder Entri Data dapat memasukkan data dari survei telepon dalam format kode ke dalam database. Encoder Entri Data dapat memasukkan jumlah pembayaran dari dokumen tender legal dari lembaga keuangan ke dalam database. Encoder Manual dapat secara manual memindai tag kode pada bagasi yang tidak terjawab oleh sistem otomatis. Perangkat lunak pengkodean medis  EncoderPro mencari kode medis ICD-9-CM , CPT , dan HCPCS Level II, untuk meningkatkan akurasi dan memungkinkan kemudahan audit untuk kepatuhan. Transduser  Transduser (seperti encoders optik atau magnetik) posisi atau orientasi rasa untuk digunakan sebagai referensi atau umpan balik aktif untuk mengendalikan posisi: Encoder putar mengubah posisi putar ke sinyal analog (misalnya, kuadratur analog) atau sinyal digital (mis. Digital quadrature, 32-bit parallel, atau USB). Encoder linier juga mengubah posisi linier menjadi sinyal elektronik. Encoders semacam itu bisa berupa absolut atau inkremental. Sinyal dari encoder absolut memberikan posisi yang tidak ambigu dalam rentang perjalanan tanpa memerlukan pengetahuan tentang posisi sebelumnya. Sinyal dari encoder inkremental bersifat siklis, sehingga ambigu, dan membutuhkan penghitungan siklus untuk mempertahankan posisi absolut dalam rentang perjalanan. Keduanya dapat memberikan akurasi yang sama, namun encoder absolut lebih kuat terhadap interupsi sinyal transduser. Telekomunikasi  Perangkat yang digunakan untuk mengubah sinyal (seperti bitstream ) atau data menjadi kode . Sirkuit elektronik  Sebuah encoder sederhana menetapkan kode biner ke jalur input aktif. Encoder prioritas menetapkan prioritas input yang bersaing (seperti permintaan interupsi) dengan mengeluarkan kode biner yang merupakan input aktif dengan prioritas tertinggi. Untuk memproduksi n no. Dari output bila ada 2 ^ n no. 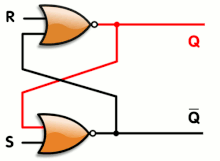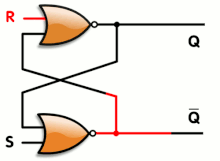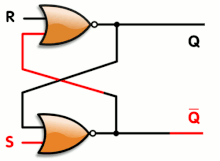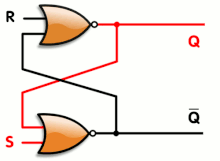Dari inpu Flip-flop R1, R2 = 1 kΩ, R3, R4 = 10 kΩ Sebuah Flip Flop RS, yang dihubungkan dengan Gerbang logika NOR]. Pada elektronik, Flip-Flop atau latch merupakan sirkuit elektronik yang memiliki dua arus stabil dan dapat digunakan untuk menyimpan informasi. Sebuah flip-flop merupakan multivibrator-dwistabil. Sirkuit dapat dibuat untuk mengubah arus dengan sinyal yang dimasukkan pada satu atau lebih input kontrol dan akan memiliki satu atau dua output. Ini merupakan elemen penyimpanan dasar pada Logika Sekuensial. Flip-flop dan latch merupakan bangunan penting dalam sistem elektronik digital yang digunakan pada komputer, komunikasi dan tipe lain dari sistem. Flip-flop dan latch digunakan sebagai elemen penyimpan data, seperti penyimpan data yang dapat digunakan untuk menyimpan memori, seperti sirkuit yang dijelaskan pada logika sekuensial. Ketika menggunakan Read-only Memory, output dan keadaan selanjutnya tidak hanya bergantung pada input awalnya saja, namun pula pada keadaan yang sekarang. Flip-flops juga dapat digunakan untuk menghitung detak, dan untuk mengsinkronisasikan input signal waktu variable untuk beberapa signal waktu yang direferensi. Flip-flop dapat digunakan secara sederhana yaitu dengan menggunakan clock; sedangkan yang paling sederhana dinamakan latch.[1] Kata "latch" lebih biasa digunakan untuk menyimpan data yang ada, sementara clocked devices dapat dikategorikan sebagai flip flop.[2] Flip-flop dan latch digunakan sebagai elemen penyimpanan data. Penyimpanan data ini digunakan untuk menyimpan state (keadaan) pada ilmu komputer, dan sirkuit ini merupakan logika sekuensial. Saat digunakan di mesin finite-state, hasil keluaran dan state selanjutnya bergantung bukan hanya kepada keadaannya saat ini, namun juga kepada state saat ini (dan, karena itu, masukan sebelumnya). Sirkuit juga dapat digunakan untuk menghitung bunyi teratur dan sinkronisasi sinyal. Daftar isi   [sembunyikan]  1Sejarah 2Jenis-jenis flip-flop 3Catatan kaki 4Pranala luar SEJARAH Skematik Flip-flop dari Patent Eccles dan Jordan Paten yang diberikan pada tahun 1918, satu gambar dari amplifier dengan pola balik positif, dan pasangan silang simetrik yang lain Flip-flop elektronik pertama ditemukan pada tahun 1918 oleh William Eccless dan F. W. Jordan[3][4][5] Awalnya dinamai Sirkui Pemicu Eccles-Jordan dan berisi dua elemen aktif (tabung vakum).[6] Seperti versi sirkuit dan transistornya yang sering dijumpai pada komputer walaupun setelah penemuan dari sirkuit integrasi, melalui flip flop yang dibuat dari gerbang logika yang kita kenal sekarang.[7][8] Early flip-flops were known variously as trigger circuits or multivibrators.</ref> JENIS-JENIS FLIP-FLOP Flip-flop dapat dibagi dalam beberapa jenis umum: SR ("set-reset"), D ("data" atau "delay" [9] ), T ("toggle"), dan jenis JK adalah salah satu bentuk umumnya. Demultiplexer Bab 9 - Fungsi Logika Kombinasi Demultiplexer, kadangkala disingkat dmux, adalah sirkuit yang memiliki satu input dan lebih dari satu output. Hal ini digunakan ketika sirkuit ingin mengirim sinyal ke salah satu dari banyak perangkat. Deskripsi ini terdengar mirip dengan deskripsi yang diberikan untuk sebuah dekoder, namun sebuah dekoder digunakan untuk memilih di antara banyak perangkat sementara demultiplexer digunakan untuk mengirim sinyal di antara banyak perangkat. 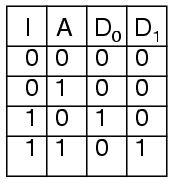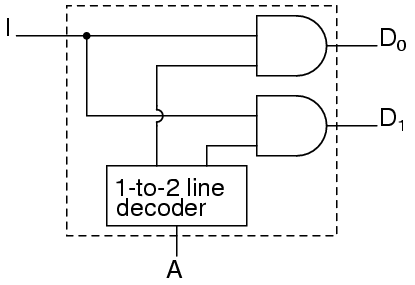Demultiplexer digunakan cukup sering sehingga memiliki simbol skematiknya sendiri Tabel kebenaran untuk demultiplexer 1-ke-2 adalah Dengan menggunakan decoder 1-ke-2 kami sebagai bagian dari rangkaian, kami dapat mengekspresikan rangkaian ini dengan mudah Sirkuit ini bisa diperluas dua cara berbeda. Anda dapat meningkatkan jumlah sinyal yang bisa ditransmisikan, atau Anda dapat meningkatkan jumlah masukan yang bisa dilalui. Untuk meningkatkan jumlah input yang bisa dilalui hanya membutuhkan decoder garis yang lebih besar. Meningkatnya jumlah sinyal yang ditransmisikan malah lebih mudah. Sebagai contoh, perangkat yang melewati satu set dua sinyal di antara empat sinyal adalah "demultiplekser 1-ke-2 dua-bit". Sirkuitnya 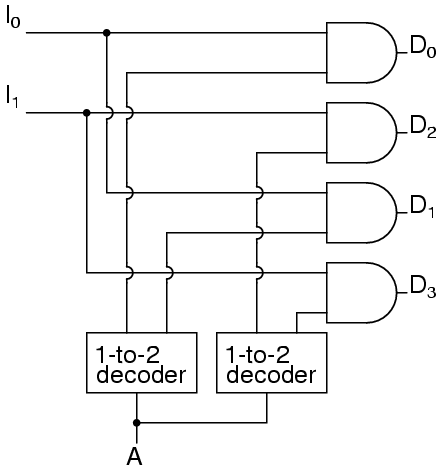Atau dengan mengekspresikan rangkaian sebagai Menunjukkan bahwa itu bisa menjadi dua demultiplexer 1-ke-2 satu bit tanpa mengubah perilaku yang diharapkan. Demultiplexer 1-ke-4 dapat dengan mudah dibangun dari demultiplexer 1-ke-2 sebagai berikut.